既存の理論を超えて、新しい世界へ　～情報幾何学の世界～

情報の幾何学とは

私は計算機科学によってより豊かになった未来を夢みて、情報と幾何学の研究を行っています。この研究の先には既存の理論を越えて初めて見える、新しい世界があると信じているからです。

私たちは言語を使って世界を認識しており、時には言語の違いが認識の違いにつながることがあります。幾何学そのものも一種の言語です。この幾何学という言語の大きな特徴として、人間がより直観的に世界を理解できる、というものがあります。これは幾何学においては、オブジェクトを定義する座標系の選択は不変であるべきだからです。座標は計算を容易にすることを目的に選ばれることがあります。その純粋さにより、幾何学は情報空間の構造の多様性を本質的にダイナミックに捉えることができます。

これは幾何学では、オブジェクトを定義するため座標系の選択不変である必要があるためです。幾何学では、オブジェクトを定義する座標系の選択は不変であるべきです。

歴史的にみても、この幾何学という言語で世界を改めて捉えようとしたとき、そこに新たな視点や切り口があることに気が付きます。例えばケプラーは最初に望遠鏡で収集した実証データから惑星運動の3つの法則を提唱しました。これらの法則は後に、ニュートン力学から理論的に導かれました。現在では、幾何学的力学はシンプレクティック幾何学やコンタクト幾何学に依拠しており、動的システムを本質的に分析するために用いられています。同様に、アインシュタインは4次元における重力をモデル化するためにリーマン幾何学を活用しました。

私は、幾何学の視点で世界を改めてみたときに生まれる理論を探求し、これらの新しい洞察に基づいて新技術を開発しています。

日常生活において、私たちはさまざまな種類の幾何学を通して世界を認識しています。以下に4つの例を紹介します（図1）：

新しい家に引っ越す際、私たちはお馴染みのユークリッド幾何学を使って箱をトラックに積み込みます。
電車に乗っている時、平行な線路が地平線で一点に収束するのを見ることができます。この時、私たちの脳はこの視覚情報を説明するために暗黙のうちに幾何モデルを投射モデルに切り替えています。
ニューヨークのマンハッタンでタクシーに乗る時、2点間の距離をユークリッド距離ではなく、L1幾何学に基づいて考えます。ここでは、点p1=(x1,y1)と点p2=(x2,y2)の距離は|x1-x2|+|y1-y2|と考えられます。これは、街路が格子状に配置されているためです。
大陸間を飛行する際、私たちは飛行機の軌道を2次元のメルカトル図法の地図上で直線ではなく、測地線と呼ばれる曲線として視覚化します。これは、飛行機が地球を囲む大円の弧に沿って飛行していることを示しています。

図1. 日常生活における様々な幾何学

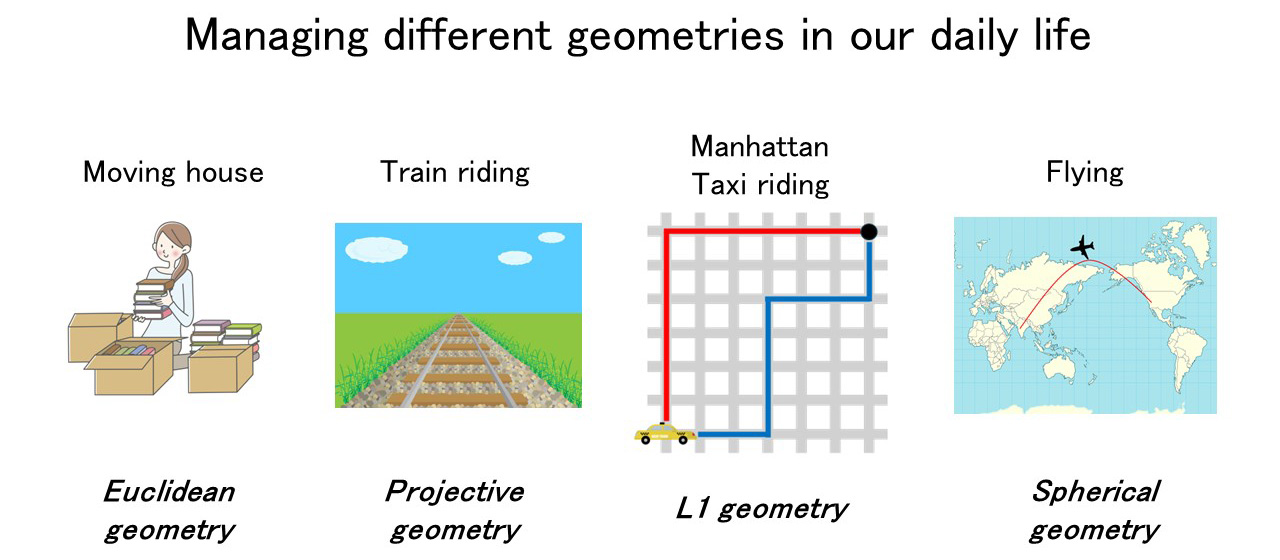
情報幾何学において（https://franknielsen.github.io/IG/index.htmlを参照）、私たちの空間は物理的なものではなく、本質的には統計的なものです。つまり、空間は確率モデルの統計モデルを表しており、データからその空間内で適切なモデルを推測することを目指します。この幾何学的視点により、効率的なアルゴリズムを構築することが可能です（図2）。情報幾何学は、信号処理（独立成分分析やレーダー処理など）、機械学習（自然勾配を用いた深層学習）、音声処理（幾何学的因子分解）、医用画像処理（拡散テンソルイメージング）など、多くの応用分野で利用されています。

図2. 幾何学的、統計学的平均の可視化

理論の「壁」を超える

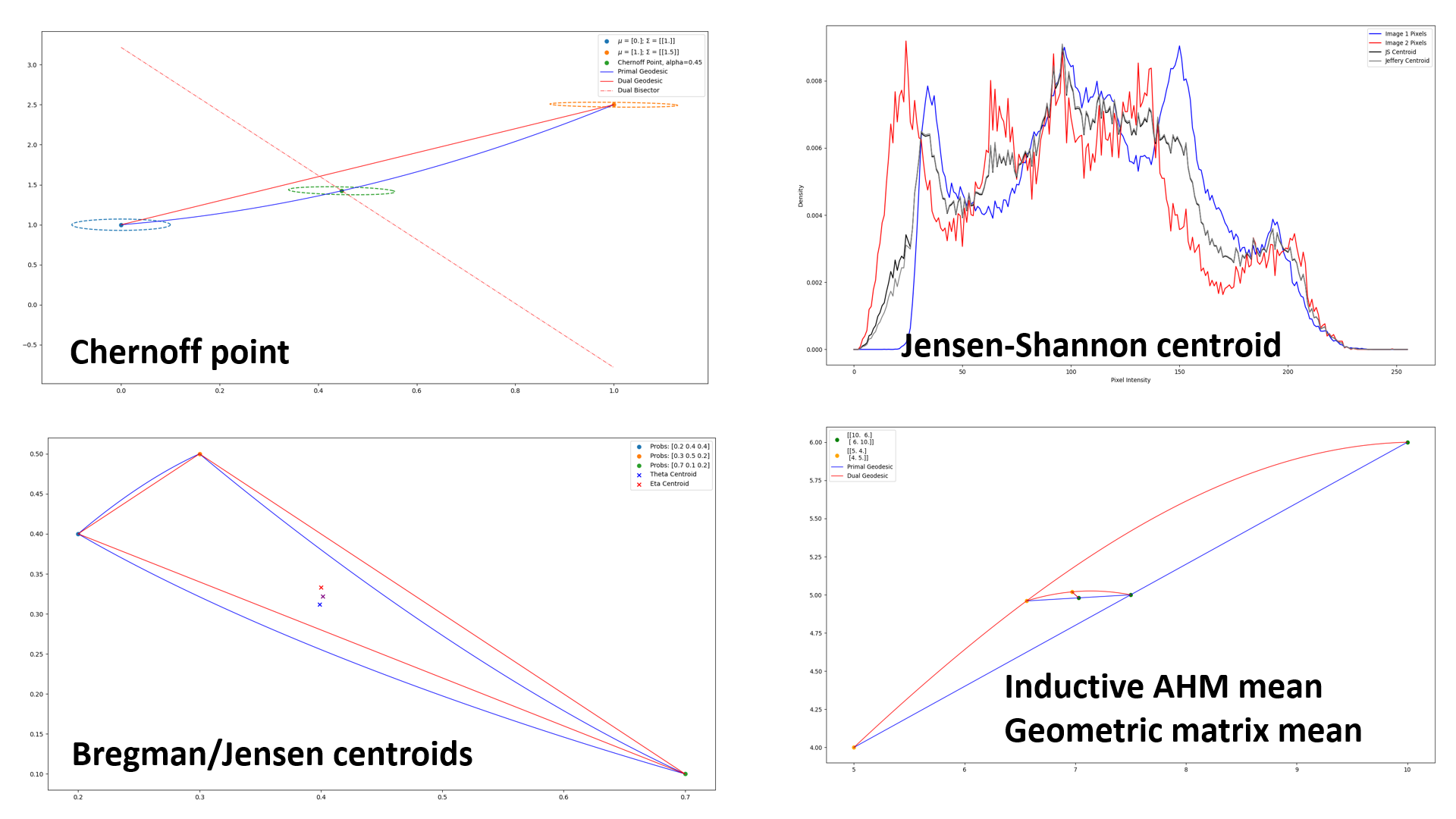
では、どのようにしたら既存の理論を超えることができるのでしょうか。そのためには、既存の理論の限界となる「壁」を見つけ、触れるようにすることが重要であり、これこそが数学者の使命だと考えています。機械学習と人工知能の分野では、データセットからモデルをどのように学習するのか？データセットから情報をどのように抽出するのか？モデルの性能と適合の良さをどのように比較するのか？大きなモデルをどのように単純化するのか？など根本的な問いが多くあります。私は現在の理論によって築かれた既存の壁を乗り越えることを目指し、これらの問題に対処する原則を追求しています。私の研究は、機械学習、データサイエンス、ビジュアルコンピューティング、人工知能といった幅広い分野に適用される幾何学的科学に及んでいます。幾何学は最先端の計算手法を提供します（図3）。私が取り組んでいるのは、本質的に非ユークリッドで、高次元でノイズが多く、大規模で異種混合の動的データセットです。

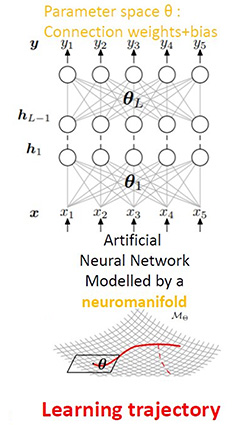
さらに、データセットの規則性と多様性の両方を捉える高度なモデルや学習機械を構築するために、幾何学的な計算手法やツールボックスを開発しています。幾何学は最も高度な微積分を提供します。例えば、我々は多様体上で偏微分方程式を定義し、それを解くことができます。これは、曲面上の偏微分方程式を解くことに等しいです。幾何学の言語と論理は、機械学習や人工知能のための新しい強力な技術を構築するインスピレーションを与えてくれます。例えば、深層ニューラルネットワーク（DNN）を学習する際、与えられた損失関数を最小化するDNNのパラメータを探します。パラメータの集合は「ニューロマニフォールド」を形成します。学習の動態をニューロマニフォールド上の軌跡として視覚化し、性能保証と不変性を備えた優れたパラメータを見つけるための高速最適化方法を設計します。

情報幾何学の未来

Geometric Science of Information (GSI, https://franknielsen.github.io/GSI/) という学会を2013年より組織し、情報の幾何学的科学のコミュニティを形成しています（2023年には第6回目の開催を行いました。写真はGSI’23の参加者です。）年々参加者が増え、コミュニティはどんどん広がっています。データ、モデル、情報、そして幾何学の関係が評価され、人々に受け入れられ始めていると感じています。